쏚쏚스포이드

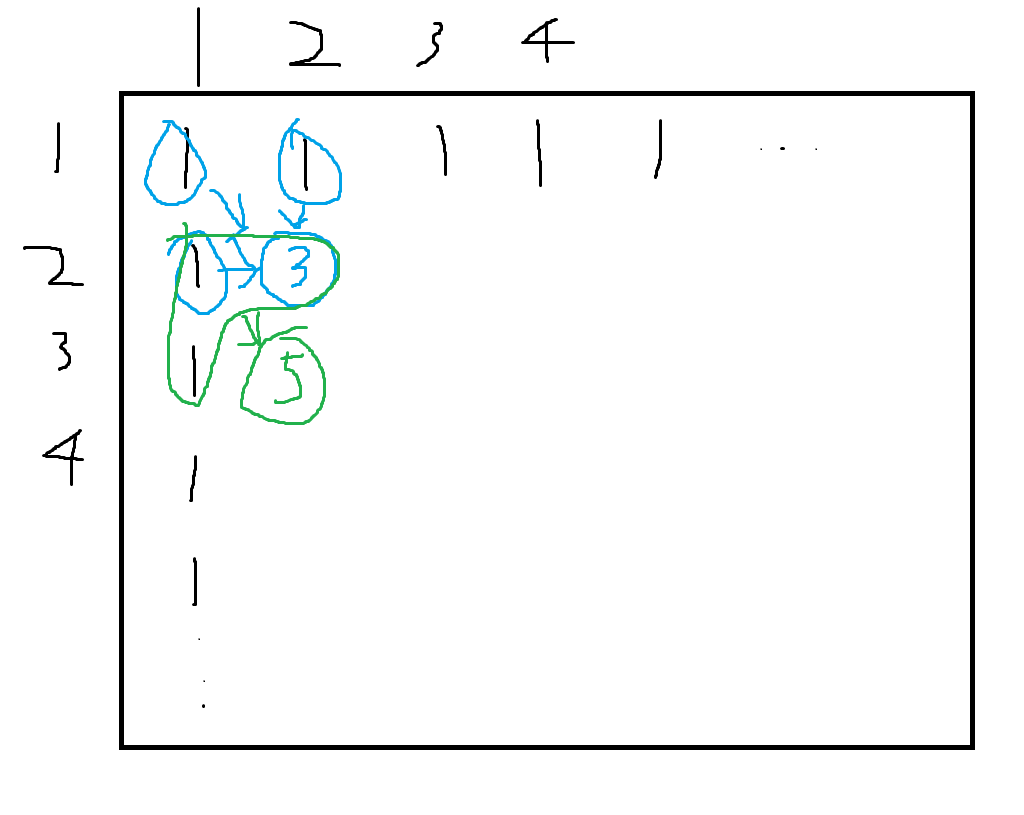
백준 포도주 시식

https://www.acmicpc.net/problem/2156

접근 방식

조건 : 연속으로 놓여 있는 3잔을 모두 마실 수는 없음

최초에 값을 초기화할 때 앞의 2개의 잔을 모두 마실 필요가 있나? x

마셨을 때 : 1

마시지 않았을 때 0

기준으로 표현하자면,

경우의 수는 110, 101, 011로 좁혀지고, 010은 고려대상이 아님

구현 방법

• DP배열에서 위 접근방식을 적용하면 해결됨

⇒

• 바텀업으로 값을 채워나감
• 최초 값은 index 2까지 초기화
  • 0 : 1
  • 1 : 11
  • 2 : 101, 110, 011
• 이후 점화식을 코드로 구현
  • i index 기준으로 봤을 때 각 경우의 수는 아래와 같이 표현됨
  • 110 : dp[i-1]
  • 101 : dp[i-2] + arr[i]
  • 011 : dp[i-3] + arr[i-1] + arr[i]

풀이

import java.io.*;
import java.util.*;

public class p2156 {
    static int[] arr;
    static int[] dp;

    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());

        arr = new int[n];
        dp = new int[n];

        for(int i = 0; i < n; i++){
            arr[i] = Integer.parseInt(br.readLine());
        }

        if(n == 1){
            System.out.println(arr[0]);
            return;
        }

        if(n == 2){
            System.out.println(arr[0] + arr[1]);
            return;
        }

        dp[0] = arr[0];
        dp[1] = arr[0] + arr[1];
        dp[2] = Integer.max(dp[1],
                Integer.max(dp[0] + arr[2], // 101
                        arr[1] + arr[2])); // 011

        for(int i = 3; i < n; i++){
            dp[i] = Integer.max(dp[i-1], // 110
                    Integer.max(dp[i-2] + arr[i], // 101
                            dp[i-3] + arr[i-1] + arr[i])); // 011
        }

        System.out.println(dp[n-1]);
    }
}

후기

점화식을 세워서 진행하는 바텀업 DP 문제는 경우의 수를 어떻게 잘 구현 해야할지 머릿속에서 잘 구상해야하는데 이게 아직도 어려운 것 같다.

14494번 다이나믹이 뭐예요?

https://www.acmicpc.net/problem/14494

Comment

DP문제의 기초격 문제

DP는 기초라고해도 왜이리 생각하기 어려운지 모르겠다..

hint

dp배열의 저장값 : 해당 지점에 도달하는 경우의 수

점화식 : 우측, 하단, 우하단 세가지 경우의 수를 활용

Solution

DP의 기초격 문제라 그런가 DP를 조금 맛본 상태에서 접했더니 점화식이 생각났던 얼마안되는 문제

먼저 dp배열을 만들고 해당 dp배열의 상단(우측으로만 진행하는 경우의 수) 하단(아래로만 진행하는 경우의 수)의 값은 도달하는 방법이 한가지 뿐이다. 때문에 먼저 초기화해서 쭉 1로 채워준 후에 해당 값을 가지고 남은 dp배열 모두를 채워나가면 되는데, 점화식은 위에 hint에 적었던 우측, 하단, 우하단 을 받는 이전dp배열을 가져오면 된다.

즉, dp[i][j] = dp[i - 1][j] + dp[i][j-1] + dp[i-1][j-1]; 로 해결이 된다

그림예시